pvlib.shading.tracker_shaded_fraction#
- pvlib.shading.tracker_shaded_fraction(tracker_theta, gcr, projected_solar_zenith, cross_axis_slope=0)[source]#
Shaded fraction for trackers with a common angle on an east-west slope.
- Parameters
tracker_theta (numeric) – The tracker rotation angle in degrees from horizontal.
gcr (float) – The ground coverage ratio as a fraction equal to the collector width over the horizontal row-to-row pitch.
projected_solar_zenith (numeric) – Zenith angle in degrees of the solar vector projected into the plane perpendicular to the tracker axes.
cross_axis_slope (float, default 0) – Angle of the plane containing the tracker axes in degrees from horizontal.
- Returns
shaded_fraction (numeric) – The fraction of the collector width shaded by an adjacent row. A value of 1 is completely shaded and zero is no shade.
See also
The shaded fraction is derived using trigonometery and similar triangles from the tracker rotation \(\beta\), the ground slope \(\theta_g\), the projected solar zenith (psz) \(\theta\), the collector width \(L\), the row-to-row pitch \(P\), and the shadow length \(z\) as shown in the image below.
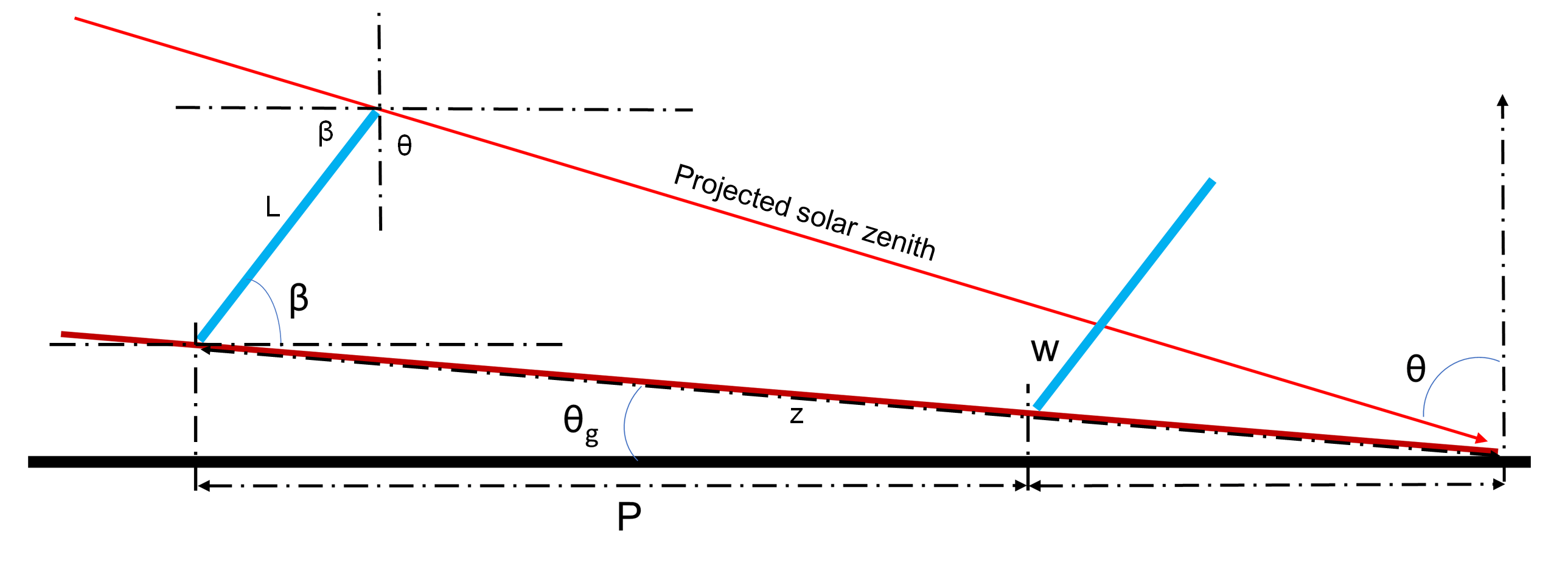
The ratio of the shadow length to the pitch, \(z/P\), is given by the following relation where the ground coverage ratio (GCR) is \(L/P\):
\[\frac{z/P}{\sin{\left(\frac{\pi}{2}-\beta+\theta\right)}} = \frac{GCR}{\sin{\left(\frac{\pi}{2}-\theta-\theta_g\right)}}\]Then the shaded fraction \(w/L\) is derived from \(z/P\) as follows:
\[\frac{w}{L} = 1 - \frac{P}{z\cos{\theta_g}}\]Finally, shade is zero if \(z\cos{\theta_g}/P \le 1\).
References
Mark A. Mikofski, “First Solar Irradiance Shade Losses on Sloped Terrain,” PVPMC, 2023